Trigonometri

Trigonometri(FireMath)

Trigonometri(Gambar)

Read More

Laporan PKL Media Kelompok 3

Assalamu'alaikum Wr.Wb

Kamis,22 Desember 2016

kami melakukan kunjungan PKL (praktik Kerja Lapangan) mata Kuliah Media dan Teknologi Pembelajaran Matematika

Kami berkunjung di sekolah MTsN Panyipatan, banyak pembelajaran dan hal menarik yang dapat di ambil dari kunjungan PKL media

ini adalah hasil laporan PKL Kelompok saya , silahkan dibaca, terimakasih :-)

Read More

Artikel Tentang Media Sosial : Facebook

Assalamu'alaikum Wr.Wb

Postingan ini mengenai tentang salah satu media sosial yang saat ini sering digunakan oleh masyarakat, yaitu Facebook

selanjutnya untuk mengetahui apa itu facebook kalian bisa membaca di file ini, silahkan dibaca dan didownload , Terimakasih :-)

Read More

Power Point Materi SMP

Assalamu'alaikum Wr.Wb

Power Point ini berisi materi Matematika SMP tentang Luas Lingkaran, silahkan dibaca dan didownload , terimakasih :-)

Read More

Power Point Bubble Short

Assalamu'alaikum Wr.Wb

Postingan kali ini saya memberikan contoh Bubble Short pada matematika, Bubble Sort adalah salah satu algoritma untuk sorting data, atau kata lainnya mengurutkan data dari yang terbesar ke yang terkecil atau sebaliknya (Ascending atau Descending). Bubble sort (metode gelembung) adalah metode/algoritma pengurutan dengan dengan cara melakukan penukaran data dengan tepat disebelahnya secara terus menerus sampai bisa dipastikan dalam satu iterasi tertentu tidak ada lagi perubahan. Jika tidak ada perubahan berarti data sudah terurut. Disebut pengurutan gelembung karena masing-masing kunci akan dengan lambat menggelembung ke posisinya yang tepat.

nah untuk melihat bagaimana Bubble Short itu silahkan dilihat pada postingan ini :-)

Read More

Menggunakan Rumus Phytagoras

Assalamu'alaikum Wr.Wb

Tahukah kalian tentang Phytagoras?

Nah pada postingan kali ini saya memberikan file tentang Phytagoras pada Segtiga, semoga bermanfaat :-)

Phytagoras pada Segitiga

Lebih dari 2000 tahun yang lalu ada penemuan yang menakjubkan tentang segitiga:

Ketika segitiga memiliki sudut kanan (90 derajat) ...

... Dan kotak yang dibuat pada masing-masing dari tiga sisi, ...

... Maka persegi terbesar memiliki wilayah yang sama persis seperti dua kotak lainnya disatukan!

Hal ini disebut "Teorema Pythagoras '" dan dapat ditulis dalam satu persamaan singkat:

$$a^2+b^2=c^2$$

catatan:

- c adalah sisi terpanjang segitiga

- a dan b adalah dua sisi lainnya

Definisi

Sisi terpanjang segitiga disebut "miring", sehingga definisi formal:

Dalam segitiga siku kanan: kuadrat dari sisi miring sama dengan jumlah kuadrat dua sisi lainnya.

Contoh: Memecahkan segitiga ini.

$$a^2+b^2=c^2$$

$$\mathrm{25}+\mathrm{144}=c^2$$

$$\mathrm{169}=c^2$$

$$c=\sqrt{\mathrm{169}}$$

$$c=13$$

Contoh dalam kehidupan sehari-hari :

Tentukan tinggi tenda jika diketahui alasnya 6m dan sisi miringnya 5m.

Lihat pada gambar !

Terlihat pada gambar, jika diketahui alas dan sisi miring tenda, nampak tenda berbentuk segitiga sama sisi , sehingga untuk menentukan tinggi tenda tersebut kita bisa menentukannya menggunakan teorema phytagoras.

Penyelesaian :

Diketahui :

Alas = CM = 6m

kita misalkan titik tengah CM adalah P

maka panjang CP = 6m : 2m = 3m

CP dan PM sama panjang, maka panjang PM = 3m

Panjang CA = 5m

Ditanya : tinggi tenda ?

Jawab :

$$a^2+b^2=c^2$$

ket :

a = tinggi = AP = ?

b = alas = CP = 3m

c = sisi miring = CA = 5m

untuk menentukan a

$$a^2+b^2=c^2$$

$$a^2=c^2-b^2$$

$$a^2=5^2-3^2$$

$$a^2=25-9$$

$$a^2=16$$

$$a=\sqrt{16}$$

$$a=4$$

Jadi tinggi tenda adalah 4m

Read More

Prisma Segitiga (Geogebra)

Bangun Ruang Prisma Segitiga

1.Pengertian dan sifat-sifat prisma segitiga

2.volume,jaring-jaring dan langkah-langkah menggambar prisma segitiga

Read More

Volume,jaring-jaring dan langkah-langkah menggambar prisma segitiga

C. Volume Prisma Segitiga

Jika sebuah balok dipotong tegak salah satu bidang diagonalnya, maka akan terbentuk dua prisma segitiga seperti gambar (a). Kedua prisma segitiga pada gambar (b) dapat digabungkan sehingga terbentuk prisma segitiga seperti gambar (c). Dengan demikian prisma pada gambar (c) dan balok pada gambar (a) memiliki tinggi, luas dan volume yang sama. Sehingga dapat dinyatakan sebagai berikut.

Rumus

$$\mathrm{Volume\; prisma\; segitiga}=\mathrm{Volume\; Balok}$$

$$=\mathrm{Luas\; Balok}\times \mathrm{Tinggi\; Balok}$$

$$=\mathrm{Luas\; alas\; prisma}\times \mathrm{Tinggi\; Prisma}$$

$$\mathrm{Volume\; prisma\; segitiga}=\mathrm{Luas\; alas}\times \mathrm{Tinggi\; Prisma}$$

atau

$$\mathrm{V\; prisma\; segitiga}=L\times t$$

$$\mathrm{V\; prisma\; segitiga}=\mathrm{Luas\; alas}\times \mathrm{Tinggi\; Prisma}$$

$$=\left(\frac{1}{2}\right)\times a\times t\times \mathrm{t\; prisma}$$

D.Jaring-jaring Prisma Segitiga

Jaring-jaring prisma segitiga merupakan rangkaian 5 buah bangun datar yang terdiri dari 2 buah segitiga yang kongruen, 3 buah persegi panjang dan jika dilipat menurut garis persekutuan dapat membentuk prisma segitiga.

Jaring-jaring prisma segitiga diperoleh dengan cara mengiris beberapa rusuk prisma tersebut sedemikian sehingga seluruh permukaan prisma terlihat. Seperti gambar di bawah ini yang merupakan alur pembuatan jaring- jaring prisma segitiga.

Langkah-langkah yang harus dilakukan dalam menggambar prisma segitiga :

1. Gambar segmen AB

2. Gambar segmen AC

3. Gambar segmen BC

4. Kemudian, dari setiap ujung segitiga ABC, yaitu titik A, B, dan C, dibuat garis lurus dengan arah vertikal. Ada tiga ruas garis yang ditarik dari ujung-ujung segitiga ABC. Tiga ruas garis itu adalah ruas garis AD, BE, dan CF yang semuanya memiliki ukuran sama panjang. Tiga ruas tersebut merupakan rusuk tegak dari prisma yang akan dibuat.

5. Langkah selanjutnya, hubungkan ujung ruas garis yang telah dibuat. Gambar segmen DF

6. Gambar segmen FE

7. Gambar segmen ED Hasilnya adalah sebuah sisi/bidang DEF yang merupakan sisi alas dari prisma segitiga. Perlu diingat garis DF digambar putus-putus karena garis tersebut terletak di belakang prisma.

Read More

Pengertian dan sifat-sifat prisma segitiga

PRISMA SEGITIGA

A. Pengertian Prisma Segitiga

Prisma merupakan bangun ruang yang dibatasi oleh dua bidang yang berhadapan yang sama dan sebangun atau kongruen dan sejajar, serta bidang-bidang lain yang berpotongan menurut rusuk-rusuk yang sejajar. Dua bidang sejajar tersebut dinamakan bidang alas dan bidang atas. Bidang-bidang lainnya disebut bidang tegak, sedangkan jarak antara kedua bidang (bidang alas dan bidang atas prisma tersebut) disebut tinggi prisma.

Prisma diberi nama berdasarkan bentuk segi-n pada bidang alas dan bidang atasnya. Prisma segi n adalah prisma yang sisi alasnya berbentuk segi n. Jadi prisma segitiga adalah prisma yang sisi alas dan sisi atasnya berbentuk segitiga.

B. Sifat- sifat Prisma Segitiga

Sifat-sifat prisma segitiga antara lain :

1. Mempunyai 5 buah sisi.

Terdiri dari 2 segitiga yang kongruen dan 3 persegi panjang (tidak harus sama besar)

2. Mempunyai 9 buah rusuk , beberapa rusuk sama panjang.

AD = BE =CF,

AB = DE,

BC = EF,

AC = DF.

3. 2 bidang kongruen dan sejajar disebut bidang alas dan atas.

4. Bentuk sisi alas dan sisi atas adalah segitiga.

5. Bentuk sisi tegak persegi panjang

6. Memilika 6 titik sudut yaitu ∠ A⁡ ,⁡ ∠ B⁡ ,⁡ ∠ C⁡ ,⁡ ∠ D⁡ ,⁡ ∠ E⁡ ,⁡ dan⁡ ∠ F⁡

Read More

Trigonometri (FireMath)

Rumus untuk tan (a+b) dan tan (a-b)

Untuk memperoleh rumus tangent jumlah dua sudut perlu mengingat kembali rumus

$$\mathrm{tan\; a}=\frac{\mathrm{sin\; a}}{\mathrm{cos\; a}}$$

dan rumus sinus dan kosinus untuk jumlah dua sudut, sehingga diperoleh.

$$\mathrm{tan\; a}=\frac{\sin \left(a+b\right)}{\cos \left(a+b\right)}$$ $$\[ =\frac{\mathrm{sin\; a\; cos\; b}+\mathrm{cos\; a\; sin\; b}}{\mathrm{cos\; a\; cos\; b}-\mathrm{sin\; a\; sin\; b}} \] \[ =\frac{\frac{\mathrm{sin\; a\; cos\; b}}{\mathrm{cos\; a\; cos\; b}}+\frac{\mathrm{cos\; a\; sin\; b}}{\mathrm{cos\; a\; cos\; b}}}{\frac{\mathrm{cos\; a\; cos\; b}}{\mathrm{cos\; a\; cos\; b}}-\frac{\mathrm{sin\; a\; sin\; b}}{\mathrm{cos\; a\; cos\; b}}} \] \[ =\frac{\frac{\mathrm{sin\; a}}{\mathrm{cos\; a}}+\frac{\mathrm{sin\; b}}{\mathrm{cos\; b}}}{1-\frac{\mathrm{sin\; a\; sin\; b}}{\mathrm{cos\; a\; cos\; b}}} \] \[ =\frac{\mathrm{tan\; a\; tan\; b}}{1-\mathrm{tan\; a\; tan\; b}} \]$$

Jadi, diperoleh rumus

$$\tan \left(a+b\right)=\frac{\mathrm{tan\; a}+\mathrm{tan\; b}}{1-\mathrm{tan\; a\; tan\; b}}$$

Dengan memandang bahwa

$$a-b=a+\left(-b\right)$$

maka dari rumus

$$\tan \left(a+b\right)$$

kita dapat menentukan rumus

$$\tan \left(a-b\right)$$

dengan langkah-langkah sebagai berikut.

$$\tan \left(a-b\right)=\tan \left(a+\left(-b\right)\right)$$ $$=\frac{\mathrm{tan\; a}+\tan \left(-b\right)}{1-\mathrm{tan\; a}\tan \left(-b\right)}$$ $$=\frac{\mathrm{tan\; a}-\mathrm{tan\; b}}{1-\mathrm{tan\; a}\left(-\mathrm{tan\; b}\right)}$$ $$=\frac{\mathrm{tan\; a}-\mathrm{tan\; b}}{1+\mathrm{tan\; a\; tan\; b}}$$

Jadi, diperoleh rumus

$$\tan \left(a-b\right)=\frac{\mathrm{tan\; a}-\mathrm{tan\; b}}{1+\mathrm{tan\; a\; tan\; b}}$$

Read More

Trigonometri (Gambar)

Rumus untuk tan (a+b) dan tan (a-b)

Untuk memperoleh rumus tangent jumlah dua sudut perlu mengingat kembali rumus

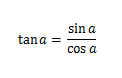
dan rumus sinus dan kosinus untuk jumlah dua sudut, sehingga diperoleh.

Jadi, diperoleh rumus

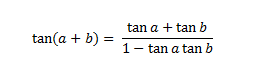
Dengan memandang bahwa

maka dari rumus

kita dapat menentukan rumus

dengan langkah-langkah sebagai berikut.

Jadi, diperoleh rumus

Read More